Intérêt du Systèmes Triphasé

1-  Définitions.

Une source triphasée est un ensemble de trois sources telles que : 

e1=E sin(wt),

e2 = E sin(wt-2π/3),
e3 = E sin(wt+2π/3).

L’ensemble (e1, e2, e3) s’appelle « système triphasé équilibré direct ». « Equilibré » signifie
que les amplitudes sont rigoureusement identiques et les déphasages entre les signaux sont de 2π/3. « Direct » indique l’ordre de succession des phases. Le système serait inverse si :
e1 = E sin(wt),

e2 = E sin(wt+2π/3),

e3 = E sin(wt-2π/3). 

2-  Intérêt du triphasé.

•   Intérêt en distribution d’énergie électrique :

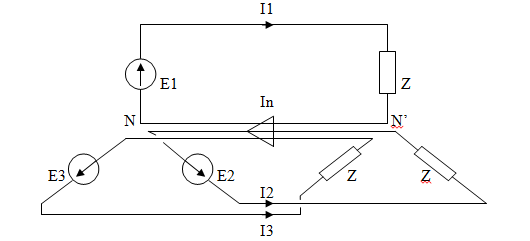
Soient trois générateurs e1,e2, e3 et trois impédances identiques à alimenter. Comparons en
monophasé et en triphasé les quantités de cuivre nécessaires à la construction des lignes.

Les courants I1, I2, I3 ont même module I. Soit une densité de courant σ. Soit L la distance entre les récepteurs et les sources.

En monophasé il faut un volume de cuivre   = 3.2.L.I/σ.

En triphasé tout se passe comme si les trois fils entre N et N’ étaient accolés en un seul

conducteur. Il circule alors dans ce conducteur N, N’ un courant In = I1+I2+I3=0. Donc si les trois sources sont reliées en un même point N et les récepteurs en un même point N’ la liaison N, N’ devient inutile. Seuls les conducteurs de phase sont nécessaire en triphasé. Il faut donc en triphasé un volume de cuivre   = 3.L.I/σ.

Conclusion en triphasé équilibré (mêmes impédances Z) il faut deux fois moins de cuivre pour construire la ligne.

Dans la pratique en distribution les charges ne sont pas tout à fait équilibrées et la connexion de neutre N, N’doit être conservée. Mais on utilise un fil de même section que pour les
phases. L’économie sur la quantité de cuivre est alors de 30%.

Il en résulte une réduction des contraintes sur les pylônes.

 •   Intérêt du triphasé pour le redressement :

Exemple d’un redressement triphasé à diodes :

                        Formes d’ondes :

Le potentiel du point A est égal à la tension simple la plus positive. Le potentiel du point B est égal à la tension simple la plus négative. La tension de sortie redressée v = van-vbn.

L’ondulation en sortie est très faible par rapport à ce que produit un pont redresseur monophasé. L’inductance de lissage à prévoir dans la charge pour que le courant I0 soit faiblement ondulé est donc nettement plus économique en triphasé. 

•   Intérêt pour les machines à induction :

Considérons un ensemble de trois bobines coplanaires et dont les axes concourent en un même point O. Ces axes forment entre eux des angles de 120°.

Chaque bobine est alimentée par une tension d’un système triphasé équilibré.

Etudions la résultante Br des inductions crées par les trois bobines au centre 0. Chaque bobine produit sur son axe une induction d’amplitude :
b1 = Bm cos wt

b2 = Bm cos(wt-2π/3)
b3 = Bm cos(wt+2π/3).

Soient Bx et By les composantes de Br sur Ox et sur Oy.

⎥Bx⎥ = Bm√3/2 cos(wt-2π/3) -Bm√3/2 cos(wt+2π/3)

⎥Bx⎥ = Bm√3/2 [- ½ coswt + √3/2 sinwt   + ½ coswt + √3/2 sinwt] ⎟Bx⎥ = (3Bm/2) sinwt.

⎥By⎥ = Bm coswt - Bm/2 cos(wt-2π/3) - Bm/2 cos(wt+2π/3)

⎥By⎥ = Bm [coswt + 1/2 coswt - √3/2 sinwt + 1/2 coswt + √3/2 sinwt] ⎥By⎥ = (3Bm/2) coswt.

On en déduit que Br est de module constant 3Bm/2 et que θ = -wt. Donc Br tourne à w. Si l’alimentation est un système triphasé inverse, le sens de rotation de Br est inversé.

Les machines tournantes triphasées utilisent cette disposition de trois bobines pour entraîner
en rotation un arbre lié à un aimant (machine synchrone) ou à une pièce conductrice (machine asynchrone).

•   Intérêt pour les transformateurs. 

Le volume de fer alloué aux jambes latérales est égal à celui de la jambe centrale.

                        En triphasé équilibré :

Sur chaque colonne on dispose un enroulement primaire de N1 spires et un enroulement secondaire de N2 spires. Les sources e1, e2, e3 sont appliquées sur chaque enroulement primaire. Chaque colonne est le siège d’une induction b1, b2, b3.

b1 = Bm cos wt

b2 = Bm cos(wt-2π/3)
b3 = Bm cos(wt+2π/3).

La somme de ces inductions est nulle à tout instant. Il n’y a donc pas besoin de jambe latérale. Il suffit de la moitié du volume de fer nécessaire à la fabrication d’un transformateur
monophasé de même puissance.

3-  Couplages.

Couplage étoile.

L’agencement de trois récepteurs ou de trois générateurs avec un point commun (le neutre) s’appelle le couplage étoile.

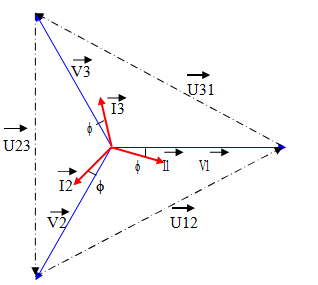
Diagramme de Fresnel :

Observations :

Dans le fil neutre le courant IN = I1 + I2 + I3 = 0.

L’amplitude d’une tension composée (U12, U23, U31) U s’exprime par rapport au module des tensions simples (V1, V2, V3) V : U = √3V .

Le courant dans les phase est le même que celui qui circule dans les branches de l’étoile. 

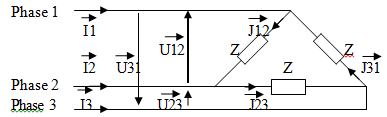
Couplage triangle.

                          Les récepteurs élémentaires sont branchés entre deux phases. Le neutre n’est pas relié. 

Diagramme de Fresnel :

  Diagramme de Fresnel :

I1 = J12 - J31                           

I2 = J23 - J12

I3 = J31 - J23                  

Observations :

L’amplitude des courants de phase (I1, I2, I3) I est liée à celle des courants de branches (J12, J23, J31) J : I = √3J.

4-  Puissances en triphasé.

•   Puissance active :

Si le couplage est étoile l’ensemble du récepteur consomme P = 3.V.I.cosϕ = √3.U.I.cosϕ. Si le couplage est triangle l’ensemble du récepteur consomme P = 3.U.J.cosϕ = √3.U.I.cosϕ. Quelque soit le couplage P = √3.U.I.cosϕ (unité W).

•   Puissance réactive :

Si le couplage est étoile l’ensemble du récepteur consomme Q = 3.V.I.sinϕ = √3.U.I.sinϕ. Si le couplage est triangle l’ensemble du récepteur consomme Q = 3.U.J.sinϕ = √3.U.I.sinϕ. Quelque soit le couplage Q = √3.U.I.sinϕ (unité var).

•   Puissance apparente :

S = √ P²+Q²           donc  S = √3.U.I           (unité VA).

•   Théorème de Boucherot.

Pour une installation comprenant plusieurs récepteurs, la puissance active totale est la somme algébrique des puissances actives consommées par chaque récepteur élémentaire, la puissance réactive totale est la somme algébrique des puissances réactives consommées par chaque
récepteur élémentaire.

Cette loi permet de connaître très rapidement le courant consommé par l’ensemble d’une installation et le facteur de puissance global. Pour cela il suffit de faire un bilan des
puissances active et réactive consommées par chaque appareil et de faire la somme
algébrique. Ensuite on trouve S = √ P²+Q², puis I = S/√3U et cosϕ = P/S.

  

5-  Mesure de puissance en triphasé.

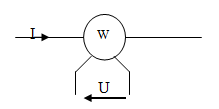
•   Le wattmètre .

  

Le wattmètre donne une indication algébrique p = U.I.cos( I,    U ) .

•   Mesure des puissances par la méthode des deux wattmètres.

L’appareil 1 indique P1 = U.I.cos( I1,  U13) = UI cos(-30°+ϕ) et cela quelque soit le couplage.

L’appareil 2 indique P2 = U.I.cos( I2,  U23) = UI cos(30°+ϕ) et cela quelque soit le couplage.

Observations :

P1 + P2 = U.I.[√3/2cosϕ + ½ sinϕ + √3/2cosϕ - ½ sinϕ] = √3U.I.cosϕ = P1 + P2 = P

√3(P1-P2) = √3U.I.[√3/2cosϕ + ½ sinϕ - √3/2cosϕ + ½ sinϕ] = √3U.I.sinϕ = √3(P1 - P2) = Q Tgϕ = √3(P1-P2)/(P1+P2).