I.1. Rappels sur la description des grandeurs sinusoïdales.
a. Ecriture des grandeurs sinusoïdales.
On écrira une tension sinusoïdale sous la forme
u = Um.cos( wt + j ) ( rigoureusement pour une tension instantanée u(t) = … )
avec Um amplitude ( V )
w pulsation ( rad.s-1 )
j phase initiale ( rad )
wt + j phase instantanée ( rad )
b. Valeur moyenne d'une grandeur périodique.
< u > = 1/T . ∫T udt ( pour un signal sinusoïdal < u > = 0 )
c. Valeur efficace d'une grandeur périodique.
C'est la racine carré de la valeur moyenne du carré de la grandeur considérée.
U = Ö 1/T . ∫T u2dt ( rms pour root mean square chez les anglo-saxons )
Pour une tension sinusoïdale on trouve :
U = Um / Ö2 ainsi on écrira souvent u = UÖ2.cos( wt + j )
La valeur efficace est celle indiquée par les voltmètres et les ampèremètres. En
électrotechnique on donne toujours la valeur efficace des tensions et des courants. Ainsi
quand on parle du réseau électrique domestique à 220 V il s'agit bel et bien de la valeur
efficace de la tension.
: au type d'appareil de mesure utilisé. Les voltmètres et ampèremètres
ferromagnétiques et électrodynamiques indiquent la valeur efficace quelque soit la
forme du signal mesuré (sinusoïdal ou non) ; tandis que les appareils magnétoélectriques ne
donnent une valeur efficace exacte que pour des grandeurs sinusoïdales.
d. Représentation vectorielle (vecteurs de Fresnel).
On peut faire correspondre à toute fonction sinusoïdale un vecteur de Fresnel partant de
l'origine du repère, de module l'amplitude de la fonction et faisant un angle égale à sa phase
instantanée avec l'axe ( Ox ) pris comme origine des phases, grâce à sa projection sur l'axe
( Ox ).
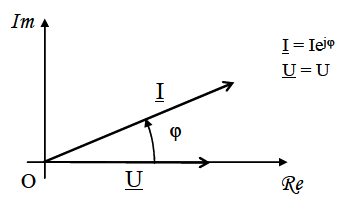
Par exemple, pour une tension u = UÖ2.cos( wt + j ) quand on dessine U le vecteur de Fresnel
associé :
a. Ecriture des grandeurs sinusoïdales.
On écrira une tension sinusoïdale sous la forme
u = Um.cos( wt + j ) ( rigoureusement pour une tension instantanée u(t) = … )
avec Um amplitude ( V )
w pulsation ( rad.s-1 )
j phase initiale ( rad )
wt + j phase instantanée ( rad )
b. Valeur moyenne d'une grandeur périodique.
< u > = 1/T . ∫T udt ( pour un signal sinusoïdal < u > = 0 )
c. Valeur efficace d'une grandeur périodique.
C'est la racine carré de la valeur moyenne du carré de la grandeur considérée.
U = Ö 1/T . ∫T u2dt ( rms pour root mean square chez les anglo-saxons )
Pour une tension sinusoïdale on trouve :
U = Um / Ö2 ainsi on écrira souvent u = UÖ2.cos( wt + j )
La valeur efficace est celle indiquée par les voltmètres et les ampèremètres. En
électrotechnique on donne toujours la valeur efficace des tensions et des courants. Ainsi
quand on parle du réseau électrique domestique à 220 V il s'agit bel et bien de la valeur
efficace de la tension.
: au type d'appareil de mesure utilisé. Les voltmètres et ampèremètres
ferromagnétiques et électrodynamiques indiquent la valeur efficace quelque soit la
forme du signal mesuré (sinusoïdal ou non) ; tandis que les appareils magnétoélectriques ne
donnent une valeur efficace exacte que pour des grandeurs sinusoïdales.
d. Représentation vectorielle (vecteurs de Fresnel).
On peut faire correspondre à toute fonction sinusoïdale un vecteur de Fresnel partant de
l'origine du repère, de module l'amplitude de la fonction et faisant un angle égale à sa phase
instantanée avec l'axe ( Ox ) pris comme origine des phases, grâce à sa projection sur l'axe
( Ox ).
Par exemple, pour une tension u = UÖ2.cos( wt + j ) quand on dessine U le vecteur de Fresnel
associé :
on retrouve bien u en projection sur ( Ox ).
Par convention on représentera les vecteurs de Fresnel à t = 0 et avec comme module la
valeur efficace de la grandeur considérée.
Par exemple, pour une tension u = UÖ2.cos( wt ) et un courant i = IÖ2.cos( wt + j ) on
dessine
j est le déphasage entre les deux vecteurs ( on prendra souvent les tensions comme référence
pour les déphasages ).
ayant la même pulsation.
e. Notation complexe.
On caractérise également les grandeurs sinusoïdales par les composantes de leurs vecteurs
représentatifs dans le plan complexe.
Addition/soustraction
L'addition ( ou la soustraction ) de deux grandeurs sinusoïdales de même pulsation,
u1 = U1Ö2.cos( wt + j1 ) et de u2 = U2Ö2.cos( wt + j2 ), est une grandeurs sinusoïdale de
même pulsation u = UÖ2.cos( wt + j ).
La détermination de u est peu évidente à effectuer par le calcul ; on obtient une solution bien
plus rapidement par construction graphique en utilisant les propriétés d'addition (ou de
soustraction) vectorielle : U = U1 + U2 , ou bien en utilisant les propriétés d'addition des
complexes.
Dérivation / Intégration
La dérivation ou l'intégration d'une grandeur sinusoïdale donne une grandeur sinusoïdale de
nature différente mais de même pulsation.
Graphiquement, dériver revient à multiplier le module de la grandeur considérée par w et à la
déphaser en avant de p/2 ; intégrer revient à diviser son module par w et à la déphaser en
arrière de p/2.
I.2. Puissances en régime monophasé.
Avec la convention de signe récepteur si la puissance est positive alors le
système considéré reçoit de l'énergie, si la puissance est négative alors il
cède de l'énergie.
a. Puissance instantanée.
p = u.i ( watt – W )
b. Puissance active (puissance moyenne).
La puissance active est la valeur moyenne de la puissance instantanée ; dans le cas de
grandeurs périodiques de période T :
P = < p > = 1/T . ∫T pdt ( watt – W )
C'est l'énergie effectivement récupérable par la charge ( sous forme de travail mécanique, de
chaleur, etc. ).
Dans le cas d'un courant et d'une tension sinusoïdales u = UÖ2.cos( wt ) et i = IÖ2.cos( wt + j)
on trouve1
p = UI.cosj + UI.cos( 2wt + j )
d’où P = UI.cosj la puissance active en régime sinusoïdal monophasé.
On retrouve ce résultat en écrivant P = U . I (produit scalaire des vecteurs associés à la
tension et à l’intensité)
c. Puissance apparente.
On définit la puissance apparente par :
S = UI ( volt-ampère – VA )
Ce qui permet d'introduire le facteur de puissance :
k = P / S ( sans unité )
En régime sinusoïdal on trouve donc k = cosj.
d. Puissance réactive en régime sinusoïdal.
La puissance réactive en régime sinusoïdal est donnée par
Q = UI.sinj ( volt-ampère réactifs – VAR )
On peut alors écrire
Q = Ö S2 – P2
et un certain nombre de relation utiles lors des résolutions d'exercices :
tanj = Q / P cosj = P / S sinj = Q / S
Vectoriellement on peut exprimer la puissance réactive sous la forme d'un produit scalaire :
Q = U' . I avec U' vecteur déphasé en arrière de p/2 par rapport à U et de
même norme.
Interprétation physique.
La puissance réactive traduit les échanges d'énergie, à valeur moyenne nulle entre une source
et une inductance ou une capacité.
Ainsi si on considère une source de tension sinusoïdale alimentant une charge purement
inductive via une ligne, la puissance active consommée par la charge est nulle. En effet dans
l'inductance la tension est en avance de j = p/2 par rapport au courant, d’où P = UI.cosj = 0.
La puissance réactive est égale à la puissance apparente Q = UI.sinj = UI = S et k = 0.
Périodiquement, l'inductance stocke une certaine énergie magnétique fournie par la source
puis la restitue ; cet échange d'énergie se fait via la ligne électrique. C'est la puissance
apparente qui permet de dimensionner la ligne, cette dernière est parcourue par l'énergie
électrique échangée et est le siège de pertes par effet Joule.
Les installations industrielles sont en général inductives (à cause des enroulements des
moteurs), de plus les compteurs électriques mesurent et permettent de facturer la puissance
active consommée par un abonné. Ainsi si le facteur de puissance d'un abonné est faible les
pertes joule dans le réseau électrique sont élevées par rapport à la puissance active qui lui est
facturée. Aussi EDF impose-t-il une valeur minimale du facteur de puissance ( un cosj
minimal ), sous peine de pénalités financières, aux utilisateurs.
Le facteur de puissance k, définit en quelque sorte un taux d'activité "utile" de la ligne.
Pour relever le facteur de puissance d'une charge inductive il suffit de placer en parallèle de la
charge des condensateurs en batterie, cette technique est illustrée figure suivante ( la tension
U étant imposée par le réseau elle n'est pas modifiée ) :
A noter que la capacité ajoutée ne consomme pas de puissance active.
e. Théorème de Boucherot.
Dans un réseau, à fréquence constante, il y a conservation de la puissance active d'une part et
de la puissance réactive d'autre part.
: le théorème de Boucherot n'est pas valable pour la puissance apparente.
Ainsi si on considère l'association de k dipôles, qu'ils soient placés en série, en parallèle ou en
toute combinaison série-parallèle possible, on a :
P = Sk Pk Q = Sk Qk S ¹ Sk Sk
avec P, Q et S les puissances actives, réactives et apparentes de l'ensemble et Pk, Qk et Sk
celles associées à chacun des dipôles.
La démonstration du théorème de Boucherot est donnée en annexe.
f. Puissance complexe.
On définit également une puissance complexe
P = U.I * = P + jQ